【印刷可能】 体積 の 求め 方 小学生 125086-体積の求め方 小学生

円すい 円錐 の体積の求め方と問題 小学数学 Irohabook
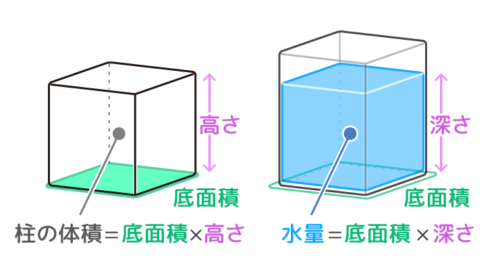
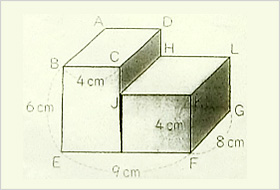
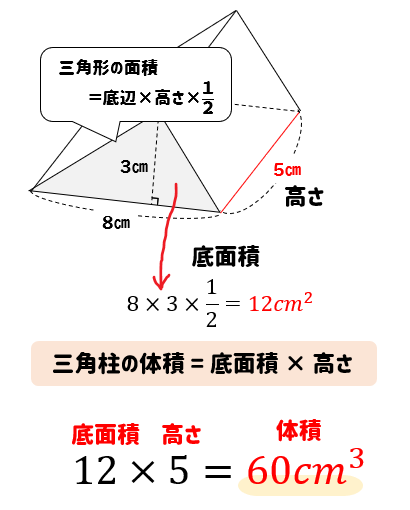
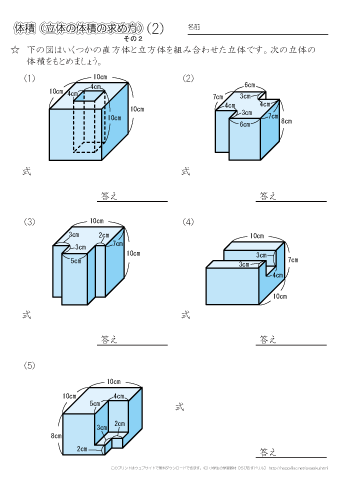
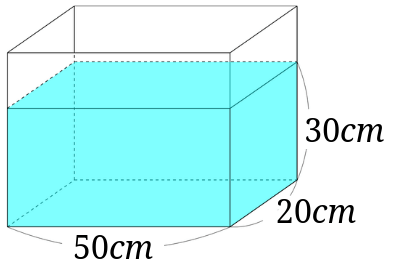
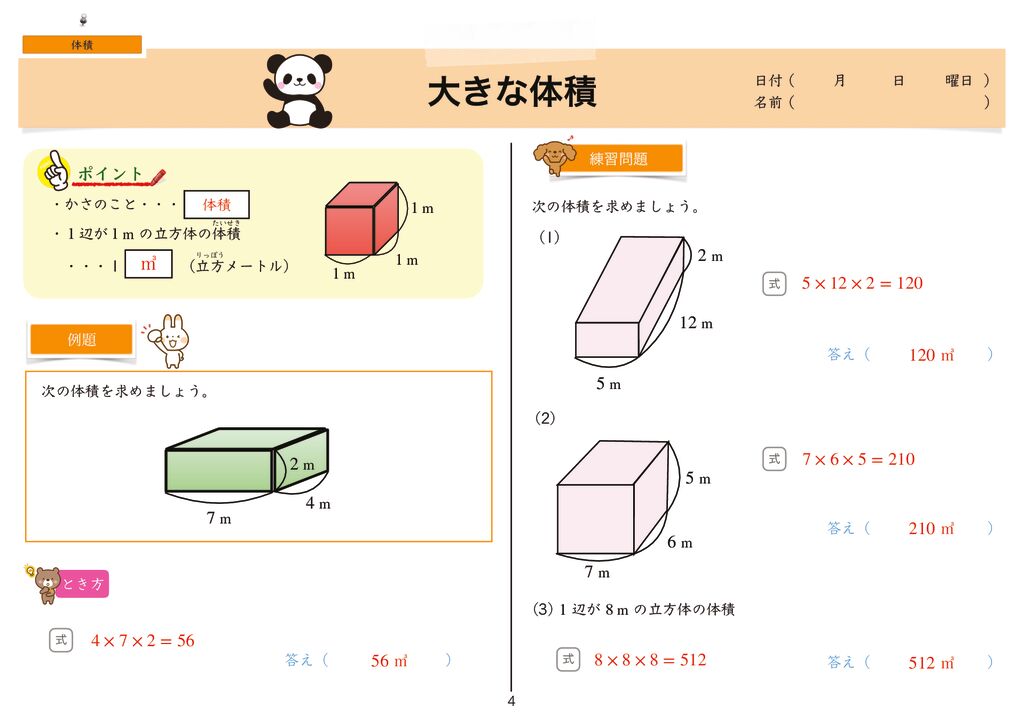
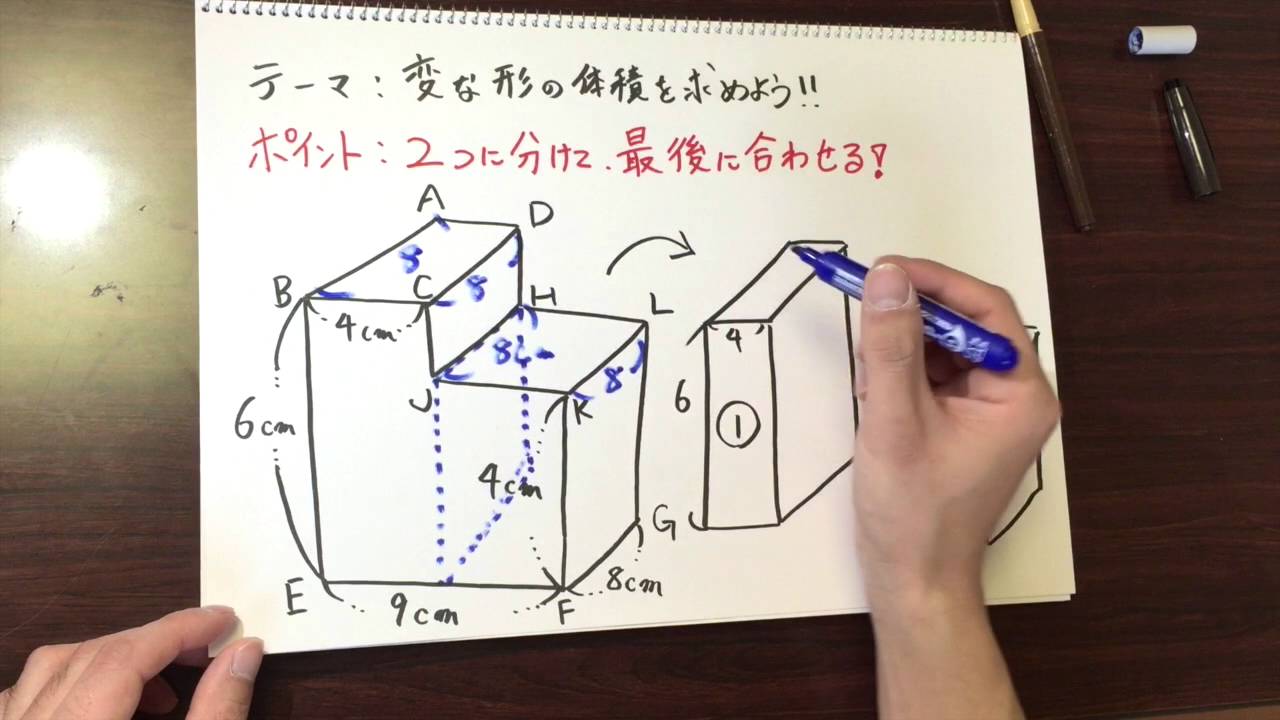
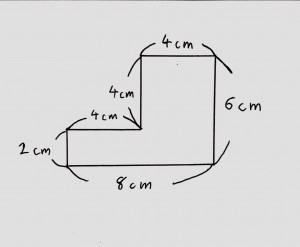
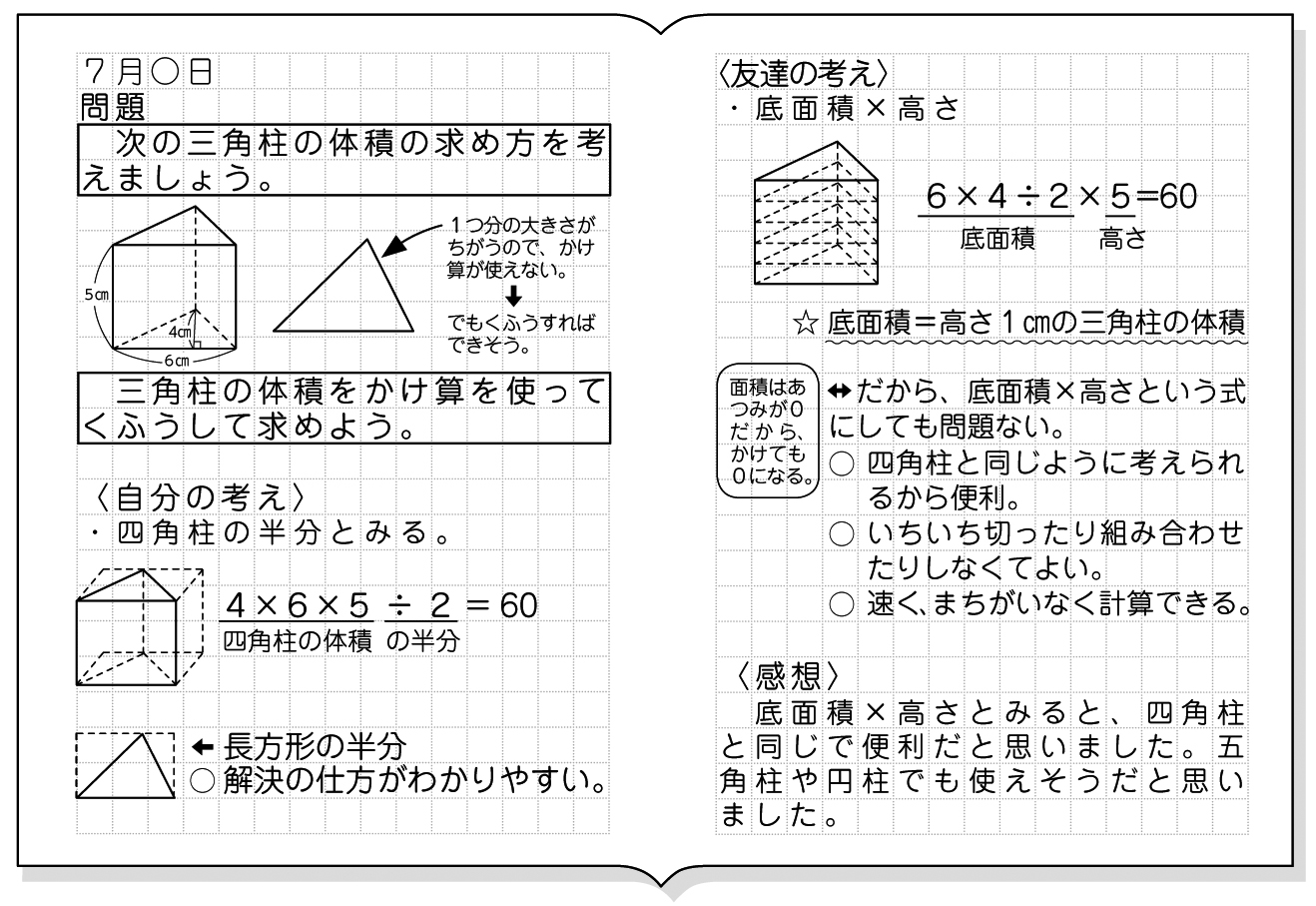
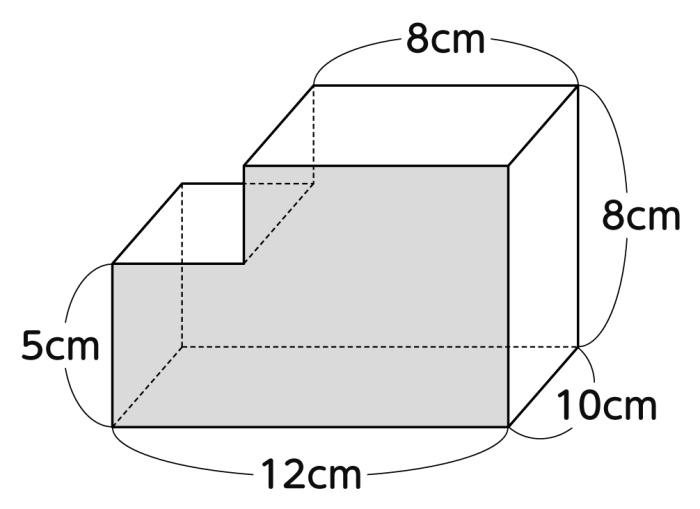
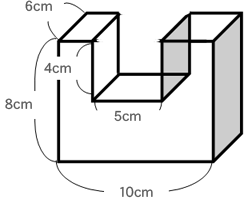
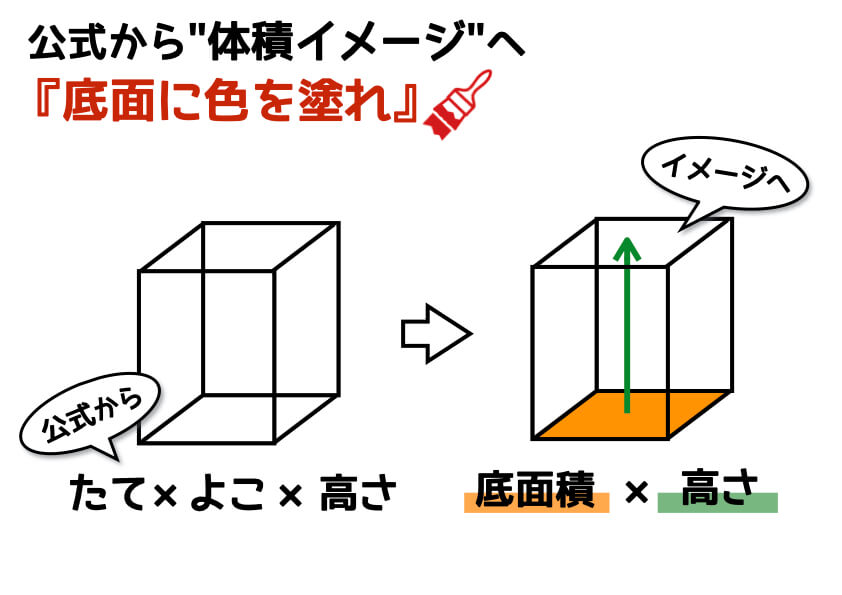
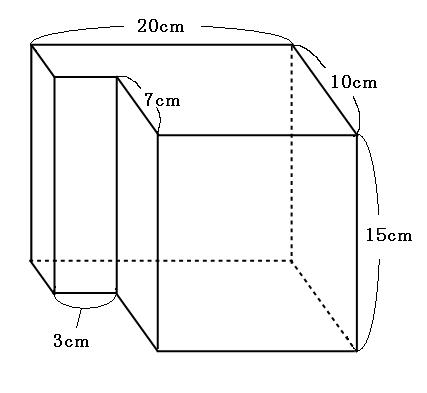
柱の体積は、「底面の面積×高さ」で求めることができます。なので、水の深さは「体積÷底面の面積」で求められます。まずは底面の面積を求めましょう。 上の図の色がついている部分が底面になるので、その面積を求めると、 10cm×10cm-4cm×5cm =100cm²-cm² 三角柱の体積は、底面である三角形の面積と三角柱の高さをかけると求めることができます。 次の例題を使って、三角柱の体積を求めてみましょう。 次の三角柱の体積を求めましょう。 まずは、底面にあたる三角形の面積を求めましょう。
体積の求め方 小学生
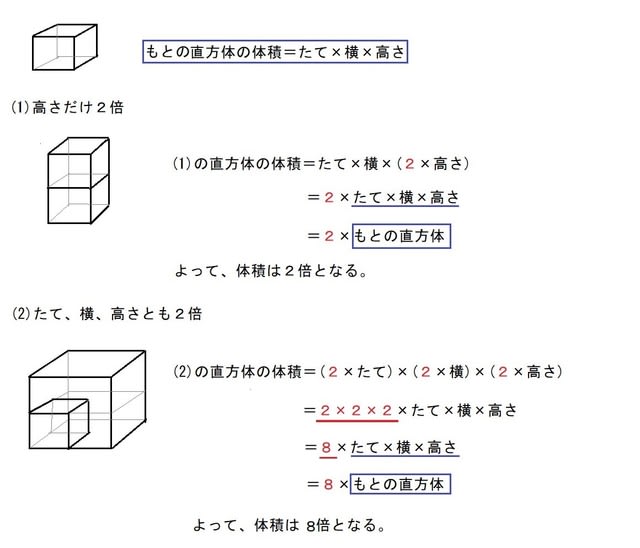
体積の求め方 小学生-5年 直方体と立方体の体積|算数イメージ動画集|大日本図書 文部科学省『教育用コンテンツ開発事業』 直方体と立方体の体積の求め方を考えます。 1辺が 1 cm の立方体が何個分あるかで求めることができます。 縦×横×高さ=直方体の体積,1辺×1辺×1辺 正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて。 台形の体積(正四角錐台)の求め方の公式!? 正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。 体積は、 1/3 h ( a^2 ab b^2) で計算できちゃうんだ。 つまり、

小学生応援
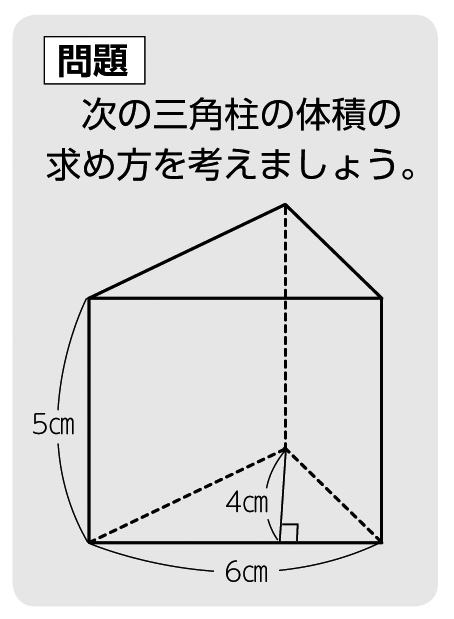
図を見てごらん。 緑色の部分が水に沈んでいる体積 だよ。 ①は水に入っている部分が無いから 浮力 は0Nだね。 ②~⑤にかけては、 水中にある体積 が増えていっているため、 浮力 が増加しているね。 ⑤~⑦は、もうすべて水中に使っているので、これ以上深くしても浮力に変化はない 円柱の体積の求め方=半径×半径×円周率×高さ 円柱に関して、体積を求める問題がよく作られます。 たとえば上の写真のように、底の円の半径と円柱の高さが示されて「この円柱の体積を求めよ」と問われます。 上の情報を元に計算の流れを説明して大きいほうの立体の体積は?(頌栄女子学院中学 13年) 小さい方の体積は大きい方の何倍?(15年 須磨学園中学) 立方体の箱の中に入るかな?(女子学院中学 08年) 四角すいB-CDIJの体積は?
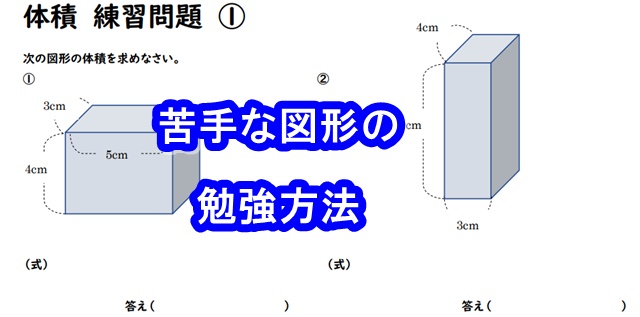
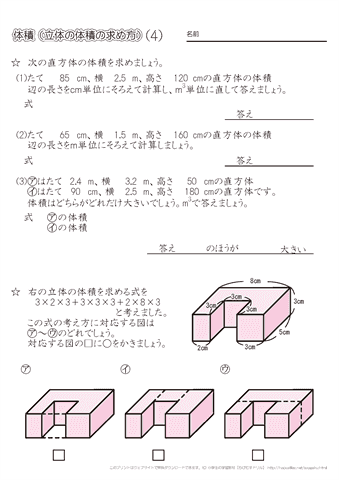
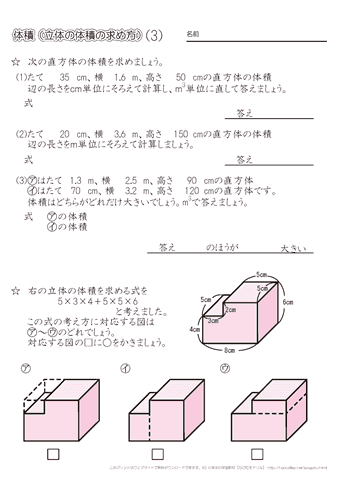
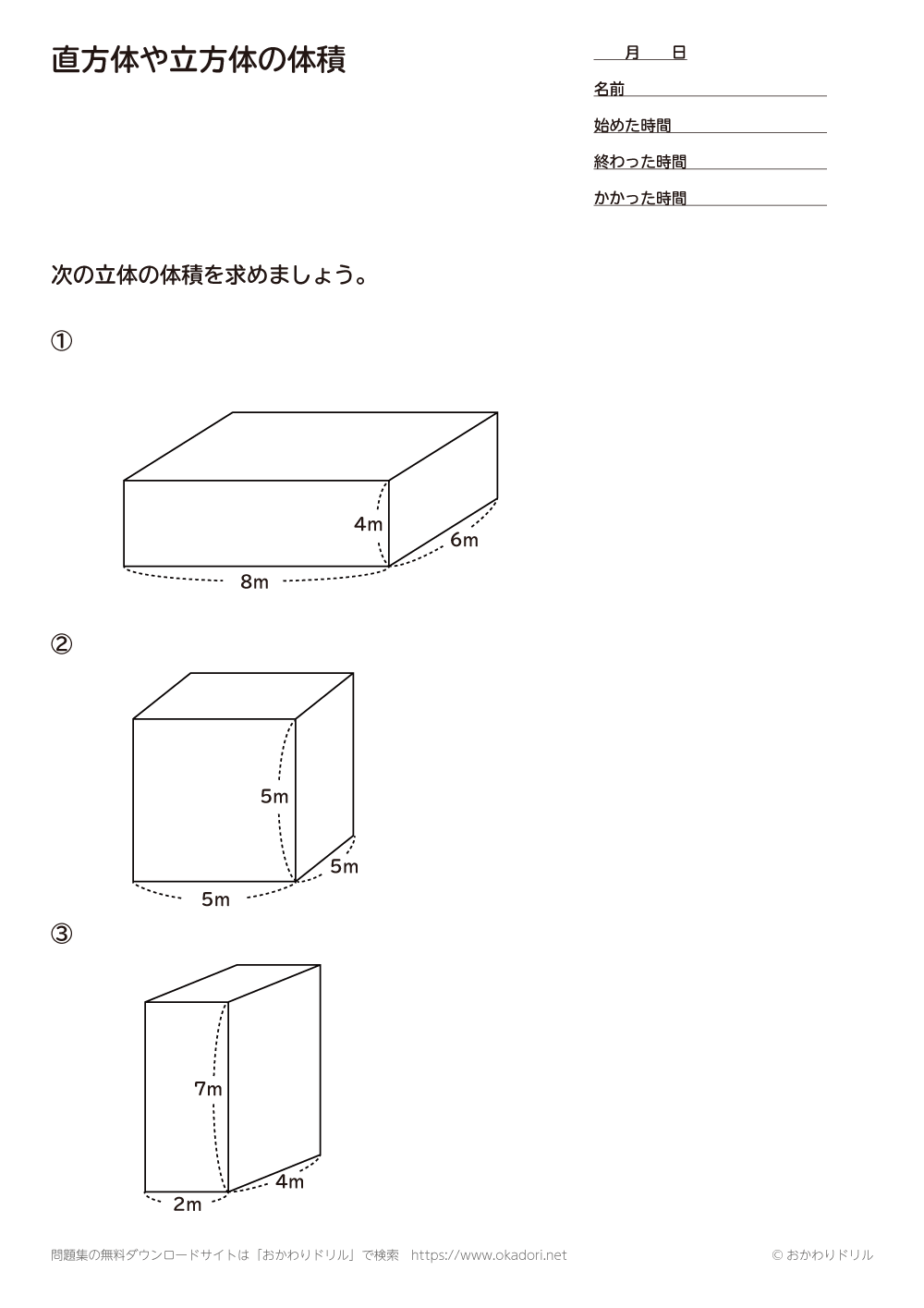
小数の表し方 整数と小数のしくみ 2 直方体や立方体の体積 体積の意味 問題一括 (6,079Kb) 解答一括 (6,325Kb) 体積の意味 直方体、立方体の体積(1) 直方体、立方体の体積(2) 直方体の横の長さと体積の関係 いろいろな体積の単位 いろいろな単位・およその単位 今回は、立方体と直方体の体積の求め方(公式)について書いていきたいと思います。 立方体の体積の求め方公式 直方体の体積の求め方公式 立方体・直方体の体積を求める問題 問題① 《立方体の体積の求め方》 問題② 《立方体の体積の求め方》 問題③ 《直方体の体積の求め方 円錐の表面積は、上の公式を覚えておけば楽勝だよ♪ それでは、例題を使って円錐の表面積の求め方を確認してみましょう。 次の円錐の表面積を求めなさい。 まずは公式にしたがって円錐の底面積を求めましょう。 底面積 次は母線と半径をかけて
体積の求め方 小学生のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
「体積の求め方 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「体積の求め方 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「体積の求め方 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「体積の求め方 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「体積の求め方 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「体積の求め方 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「体積の求め方 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「体積の求め方 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「体積の求め方 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「体積の求め方 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「体積の求め方 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
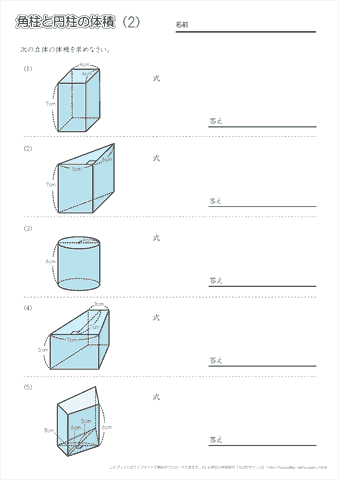
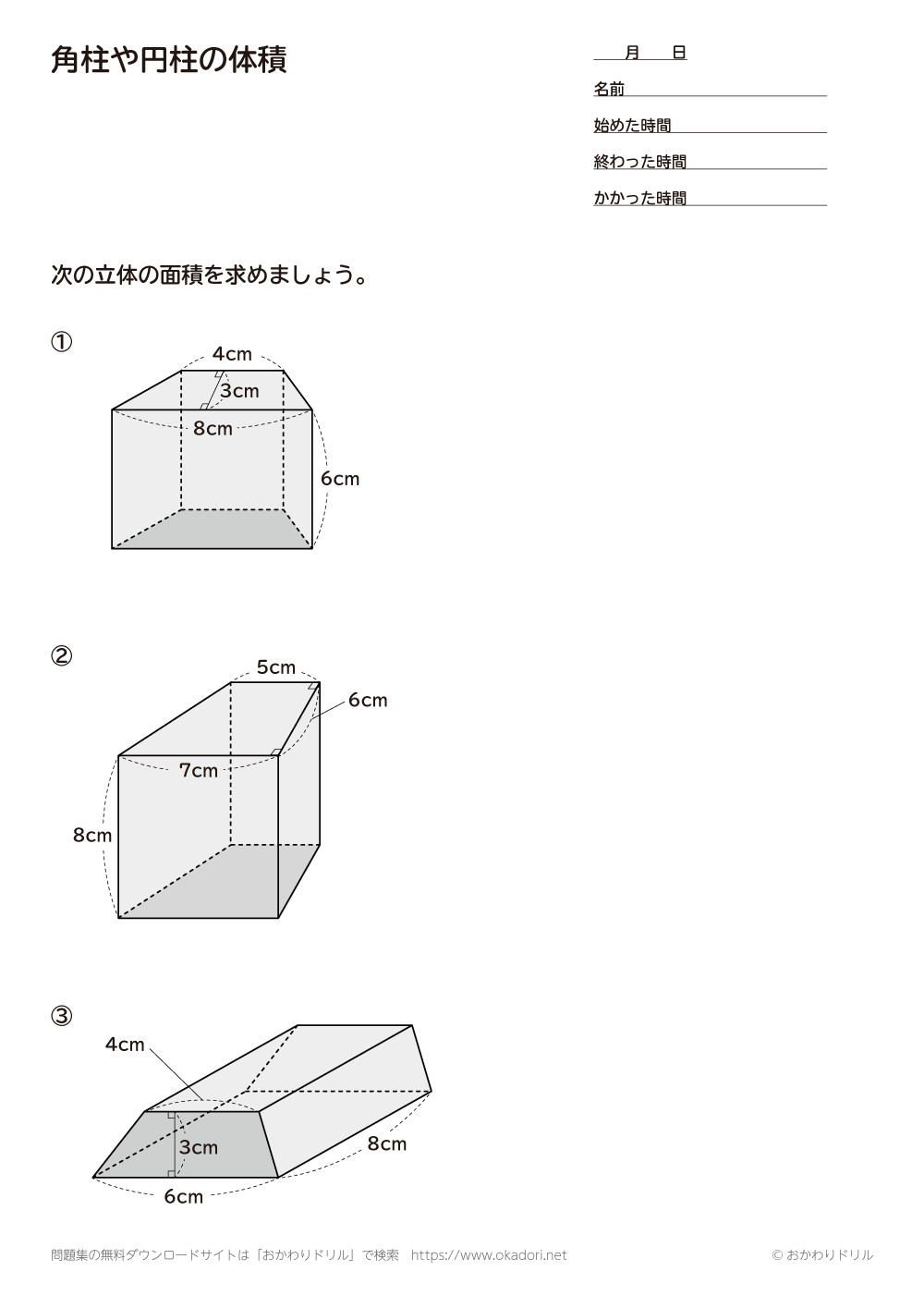
小学6年生の算数 角柱や円柱の体積の求め方・公式 問題プリント ツイート 無料ダウンロード・印刷できる、角柱・円柱の体積を求める練習問題プリント です。 角柱や円柱の名前、体積を求める公式を確認し、体積の計算をする練習を繰り返し行う 体積の求め方(立方体・長方体) 小学生 算数のノート Clearnote 表紙 1 公開日時 18年09月15日 19時46分 更新日時 19年12月13日 07時12分 小学生 算数
Incoming Term: 体積の求め方 小学生,
コメント
コメントを投稿